Konu Özeti
İçerisinde en az bir tane değişken bulunduran iki niceliğin birbirine eşitliğini ifade eden bağıntılara denklem denir. İki nicelik arasındaki büyük küçük olma durumunu belirten bağıntılara ise eşitsizlik denir. Bu iki kavramların özellikleri ve çözümleri ayrıntılı olarak incelenmiştir.
Denklemler
İçerisinde en az bir tane değişken bulunduran iki niceliğin birbirine eşitliğini ifade eden bağıntılara denklem denir.
Birinci Dereceden Bir Bilinmeyenli Denklemler
a, b R ve a 0 için ax + b = 0 şeklindeki ifadelere, x değişkenine (bilinmeyene) bağlı birinci dereceden bir bilinmeyenli denklem denir. a ve b denklemi katsayıları, x’e değişken denir. Denklemin derecesi değişkenin kuvvetine göre değişir.
Denklemi sağlayan x değerinin bulunmasına denklemi çözmek, denklemi sağlayan x R değerine denklemin kökü denir. Denklemin köklerinden oluşan kümeye, denklemin çözüm kümesi (Ç veya ÇK) denir.
- ax + b = 0 ifadesindeki terimlerde x değişkeninin üssü 1 olduğundan birinci dereceden bir denklem olur.
- ax + b = 0 denkleminde a 0 ise denklemin R de tek kökü vardır. Ç={-} olur.
- ax + b = 0 denkleminde çözüm kümesi R ise a=0 ve b=0 dır.
Birinci Dereceden İki Bilinmeyenli Denklemler
a, b, c R ve a 0, b 0 için ax+by+c=0 şeklindeki ifadelere x ve y değişkenlerine bağlı birinci dereceden iki bilinmeyenli denklem denir. Birinci dereceden iki bilinmeyenli bir denklemi gerçek sayılar kümesinde sağlayan sonsuz sayıda (x, y) ikilisi vardır ve bunlara denklemin çözüm kümesi denir. Çözüm kümesi analitik düzlemde bir doğru belirtir.
Örnek: 3x + 2y =6 denklem sistemini sağlayan (x, y) ikililerinin görüntü kümesini analitik düzlemde çizelim.
Çözüm: Düzlemdeki herhangi iki noktadan yalnızca tek doğru geçer. Denklemin çözüm kümesindeki ikililer aynı doğru üzerinde olur. Bu durumda doğrunun eksenleri kestiği noktayı bularak çizim yapabiliriz.
y eksenini kestiği noktada x=0 olur ve y=3 olur.
x eksenini kestiği noktada y=0 olur ve x=2 olur.
Bu durumda 3x + 2y =6 doğrusu (0, 3) ve (2, 0) noktalarında eksenleri keser ve aşağıdaki gibi çizilir.
ax + by + c = 0 denklemi her x, y R için sağlanıyorsa (Ç=R2 ) a=0, b=0, c=0 dır.
ax +by + c = 0 denkleminin çözüm kümesi boş küme ise a=0, b=0, c 0 dır.
Basit Eşitsizlikler
a, b R olmak üzere a<b, ab, b<a ya da ba şeklindeki ifadelere basit eşitsizlik denir.
x, y, a, b R olmak üzere basit eşitsizliklerin özellikleri aşağıdaki gibidir.
Bir eşitsizliğin her iki tarafına herhangi bir reel sayı eklenir ya da çıkarılır ise eşitsizlik değişmez.
Bir eşitsizliğin her iki tarafı pozitif bir sayı ile çarpılırsa eşitsizlik yön değiştirmez. Negatif bir sayı ile çarpılırsa eşitsizlik yön değiştirir.
Bir eşitsizliğin her iki tarafı pozitif bir sayı ile bölünürse eşitsizlik yön değiştirmez. Negatif bir sayı ile bölünür ise eşitsizlik yön değiştirir.
x<y ve y<z ise x<z dir. “<” işleminin geçişme özelliği vardır.
Aynı yönlü eşitsizlikler, taraf tarafa toplanabilir. Örneğin 2<9 ve 4<7 ise 2+4 < 9+7 ve 6<11 olur. Eşitsizliklerde taraf tarafa çıkarma, çarpma bölme işlemleri yapılamaz.
Pozitif sayılar arasındaki eşitsizliklerde her iki tarafın pozitif doğal sayı kuvveti alınırsa eşitsizlik yön değiştirmez.
Negatif sayılar arasındaki eşitsizliklerde her iki tarafın tek doğal sayı kuvveti alınırsa eşitsizlik yön değiştirmez. Sıfır dışındaki çift doğal sayı kuvveti alınırsa eşitsizlik yön değiştirir.
Birinci Dereceden Bir Bilinmeyenli Eşitsizlikler
a, b R ve a 0 için ax+b≤0, ax+b<0, ax+b≥0, ax+b>0 şeklindeki ifadelere x değişkenine bağlı birinci dereceden bir bilinmeyenli eşitsizlik denir. Bu tür eşitsizliklerin çözüm kümesi, reel sayıların bir alt aralığıdır.
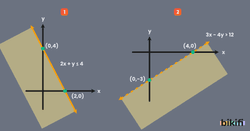
Birinci Dereceden İki Bilinmeyenli Eşitsizlikler
a, b R; a, b 0 olmak üzere ax+by+c0, ax+by+c0, ax+by+c0, ax+by+c0 şeklindeki ifadelere birinci dereceden iki bilinmeyenli eşitsizlik denir. (x, y) ikilisi eşitsizliği sağlar ve bu ikililerin kümesine eşitsizliğin çözüm kümesi denir. Çözüm kümesi analitik düzlemde boyalı olarak gösterilebilir.
ax+by+c=0 ifadesinde y, x e bağlı olarak yazılırsa by=-ax-c ve halini alır. Oluşan denklemde olarak yazılır ise denklem y=mx+n olur.
Oluşan yukarıdaki denklem ve çözüm kümesinin oluşturduğu analitik düzlem görüntüsünün özellikleri aşağıdaki gibi olur.
- y=mx+n denkleminin çözüm kümesi, doğru üzerindeki noktaları gösterir.
- y>mx+n eşitsizliğinin çözüm kümesi, y=mx+n doğrusunun üst bölgesidir.
- y<mx+n eşitsizliğinin çözüm kümesi, y=mx+n doğrusunun alt bölgesidir.
bulunması durumunda denklemin çözüm kümesinde doğru üzerindeki noktalarda yer alır ve düz çizgi olarak çizilir.
olması halinde denklemin çözüm kümesinde doğru üzerindeki noktalar yer almaz ve kesikli çizgi olarak çizilir.
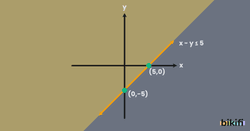
Örnek: eşitsizliğinin çözüm kümesini analitik düzlemde gösterelim
x=0 için y=-5 ve y=0 için y=5 olur. Bulunan noktalardan geçen doğru çizilir. Doğrunun analitik düzlemi iki bölgeye ayırdığı görülmektedir. Çözüm kümesinin hangi bölgeyi kapsadığını bulmak için bir nokta seçip eşitsizlikte yazılır ve sağlıyor ise o bölge taranır sağlamıyor ise diğer bölge taranır. (0, 0) noktasını denersek eğer 0-05 eşitsizliği elde edilir ve doğru olduğu görülmektedir. Bu durumda (0, 0) noktasının olduğu alan taranır.

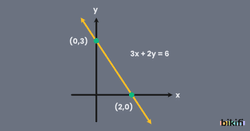
Hiç yorum yok:
Yorum Gönder
ders,plan,proje,performans,ödev