Denklemler ve Eşitsizlikler Ders Notları

Denklemler ve Eşitsizlikler Ders Notları

Birinci Dereceden İki Bilinmeyenli Denklem ve Eşitsizlik Sistemleri

Mutlak Değer

Birinci Dereceden Denklemler ve Eşitsizliklerin Çözümü

EBOB ve EKOK

Bölünebilme Kuralları

Temel Kavramlar: Sayılar

Eğitim : Ödev / Ders / Proje / Tez / Çizim

Gerçek Sayı Aralıkları

Konu Özeti

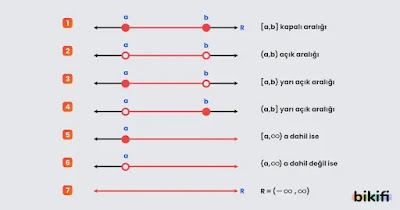
Gerçek sayı aralıkları matematikte sıklıkla kullanılan gösterimleri içermektedir. Gerçek sayılarda herhangi bir aralık belirtmek için 6 farklı yöntem vardır. Bunlar sırasıyla; kapalı aralık, açık aralık, yarı açık (yarı kapalı) aralık, üstten sınırsız aralık, alttan sınırsız aralık ve "R" aralığıdır.

Kapalı Aralık

a ve b birer gerçek sayı olmak üzere, a<b olsun. a ve b sayıları ile bu sayılar arasında kalan tüm gerçek sayılar a, b kapalı aralığını oluştururlar ve bu aralık [a, b] şeklinde gösterilir.

• [a, b]={x | a ≤ x ≤ b, x $\in$ R} (Yukarıdaki resimde 1 numaralı grafik)

Açık Aralık

a, b kapalı aralığından a ve b sayıları çıkarılırsa a, b açık aralığı elde edilir ve a, b açık aralığı (a, b) şeklinde gösterilir.

EBOB ve EKOK

Konu Özeti

İki veya daha fazla sayıyı birlikte bölebilen en büyük doğal sayıya bu sayıların en büyük ortak böleni (EBOB) denir. İki veya daha fazla sayının hepsinin birden katı olan en küçük doğal sayıya bu sayıların en küçük ortak katı (EKOK) denir. Bu değerler günlük hayattaki tekrar eden hesaplamalarda kullanılır.

En Büyük Ortak Bölen (EBOB)

İki veya daha fazla sayıyı birlikte bölebilen en büyük doğal sayıya bu sayıların en büyük ortak böleni denir ve EBOB şeklinde gösterilir.

18 ve 24 sayılarının bölenlerini incelersek

• 18 in tam sayı bölenleri: 18→{1, 2, 3, 6, 9, 18} şeklindedir.

Bölünebilme Kuralları

Konu Özeti

Tam sayılarda bölme algoritmalarından yola çıkarak devamında bölünebilme kuralları ve bazı sayılarda bölünebilme koşulları ele alınmıştır. Aynı zamanda asal çarpan ve tam sayı bölenleri de incelenmiştir

Bölme işlemi çarpma işleminin tersi olan aritmetik işlemdir. Bir bütünün istenilen sayı kadar eş parçaya ayrılması temeline dayanır.

Tam Sayılarda Bölme Algoritması

Temel Kavramlar: Sayılar

Konu Özeti

Bir çokluk belirtmek için, rakamların belirli kurallara göre bir araya getirilmesiyle oluşan ifadeye sayı denir. Temel kavramların ele alındığı bu yazıda rakam, sayı ve sayı kümeleri ele alınmıştır. Ayrıca sayı kümelerinin özellikleri anlatılmıştır.

Rakam Nedir?

Birinci dereceden bir bilinmeyenli denklemler

A. TANIM

a ve b gerçel (reel) sayılar ve a ¹ 0 olmak üzere,
ax + b = 0 eşitliğine birinci dereceden bir bilinmeyenli denklem denir.
Bu denklemi sağlayan x değerlerine denklemin kökü, denklemin kökünün oluşturduğu kümeye denklemin çözüm kümesi denir.
B. EŞİTLİĞİN ÖZELLİKLERİ