En büyük (?) asal sayı

Bugünlerde haber sitelerinde “En büyük asal sayı bulundu” türünden haberlere rastlayabilirsiniz. Bu haberlerin aslı var mı? Asal sayı nedir? En büyük asal sayı (?) bulunabilir mi? Asal sayı arayışının tarihteki örnekleri, asal sayı bulmanın bize ne yararı var ve siz sıcak evinizden bu arayışa nasıl katkıda bulunabilirsiniz? 

Asal sayı nedir? Tüm asal sayılar belirlenebilir mi? 

Asal sayılar sadece kendisine ve 1’e bölünebilen 1’den büyük doğal sayılar olarak tanımlanır. Örneğin ilk 10 asal sayı 2, 3, 5, 7, 11, 13, 17, 19, 23, 29 biçiminde sıralanır.

Acaba asal sayılar kaç tanedir? Tüm asal sayılar belirlenebilir mi?

Bir sayının asal olması için kendisinden küçük 1 dışında hiçbir sayıya bölünmemesi gerekiyor. O halde büyük bir sayının asal olma ihtimali, küçük bir sayının asal olma ihtimalinden çok daha düşük olur gibi geliyor insana! Ne de olsa kendinden küçük çok daha fazla sayı var.  Bunların hiçbirine bölünmüyor olma ihtimali de doğal olarak çok daha düşük olacaktır.

İlk tahminimiz sayılar büyüdükçe asal olma ihtimalinin giderek azalacağı yönünde. Peki bu durumda çok büyük asal sayılar olabilir mi? Yoksa belirli bir sayıdan sonra kendinden küçük çok fazla sayı olacağından bu sayının asal olma ihtimali kalmıyor olabilir mi? Yani, asallar sonlu sayıda mıdır?

Bu fikirden yola çıkarak asal sayıları sırayla bulmak için bir yöntem geliştirebiliriz. Bir kâğıda 1’den 100’e kadar bütün doğal sayıları yazalım. 1 tanım gereği asal sayı değil. 2 ise sadece kendine ve 1’e bölündüğünden ilk asal sayımız. Bundan sonra bütün çift sayıları eleyebiliriz, sonuç olarak bunlar 2’ye bölünüyor. Kalan ilk sayı 3, bir asal sayı, çünkü elenmediğinden kendinden küçük hiçbir asal sayıya (yani 2’ye) ve dolayısıyla 1 hariç hiçbir doğal sayıya bölünmüyor. Üçün katlarını eledikten sonra sırada elenmeyen ilk sayı 5, üçüncü asalımız. Bu şekilde devam ederek sırasıyla bütün asalları elde edebiliriz. Buna Eratosthenes eleği deniyor.

Erostotheles eleği – Elek çalıştıkça sağda asal sayı listesi oluşuyor (wikipedia)

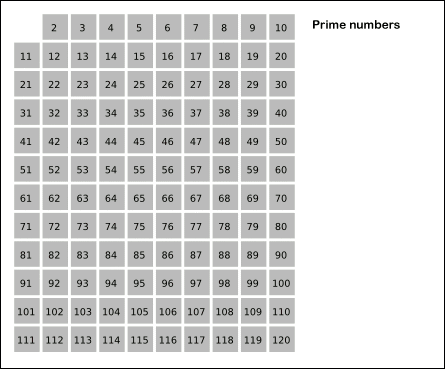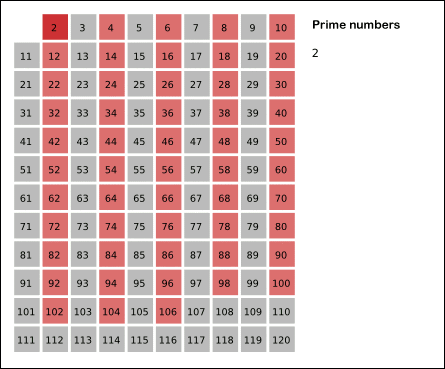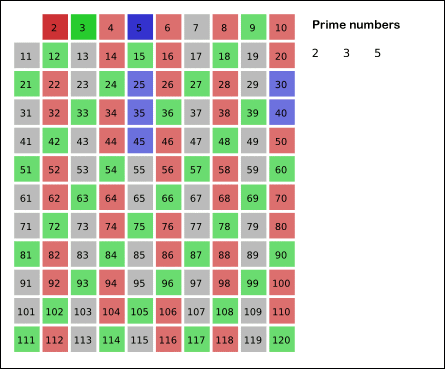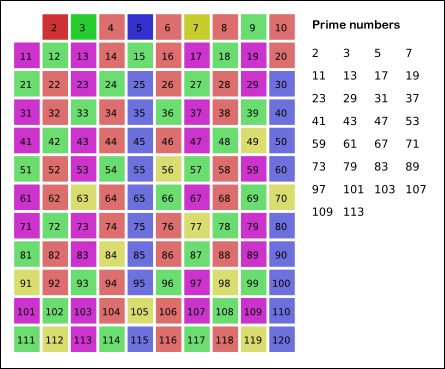
Peki bu eleme işlemini 100’de durdurmasak, tüm sayılara uygulasak, geriye kaç asal kalır? Bu sorunun cevabını bundan 2000’i aşkın yıl önce Öklid vermiş:

Sonsuz tane asal sayı vardır.

Öklid’in ispatı şu şekilde:

Sonlu tane asal içeren bir liste alalım. Bunların hepsini çarpıp 1 ekleyelim. Elde edeceğimiz sayı (buna $N$ diyelim) asal sayıysa listede olmayan bir asal sayı elde etmiş olduk. Eğer $N$ asal değilse, o zaman $N$‘yi bölen en az bir asal sayı olmak zorunda. Bu asal çarpanına da $p$ diyelim. $p$ listedeki asallardan biri olamaz, çünkü olsaydı bu durumda, $p$ hem $N-1$’i (listedeki kendisinin de dahil olduğu asalların çarpımını) hem de $N$’yi bölecekti. Dolayısıyla bu iki sayının farkını, yani 1’i de bölmek zorunda olurdu. 1’i bölen bir asal sayı olmadığına göre $p$ listedeki asallardan birisi olamaz.

Her iki durumda da listede olmayan yeni bir asal sayı ($N$ veya $p$) elde etmiş olduk. Sonlu sayıda asal içeren her liste için bu listede olmayan bir asal sayı olduğunu ispatladık. Bu da tam olarak sonsuz tane asal sayı olması gerektiğini gösterir.

Peki sonsuz tane asal sayı varsa en büyük asalın bulunması ile ilgili haberler ne anlama geliyor? Hiçbir anlama gelmiyor tabii ki. Bulunan her asaldan büyük başka asallar olduğunu (hatta sonsuz tane!) Öklid’den beri biliyoruz. Hepsini tek tek bulmak ve yazmak mümkün değil. Peki hepsini birden veren bir formül bulsak! Veya en azından hep asal sayı veren bir formül bulup sonsuz sayıda asal sayı üretsek!

Fermat’ın Mersenne’e yazdığı 25 Aralık 1640 tarihli mektup (Paul Tannery ve Charles Henry,  Fermat’ın eserleri,  1894, s 212))

Asal arayışımız

Bu arayışın örneklerinden birini Fermat’nın Mersenne’ye bundan tam 384 yıl önce (25 Aralık 1640) yazdığı bir mektupta buluyoruz. Fermat 3, 5, 17, 257, 65.537,…,  sayılarının hepsinin asal olduğunu ve bunun nedenini anlamaya çalıştığını yazmış. Yani her n doğal sayısı için

$$2^{2^n}+1$$

sayısının her zaman asal olacağını öne sürmüş (günümüzde bu sayılara Fermat sayıları deniyor). Gerçekten de ilk 5 Fermat sayısının tümü asal! Ancak 1732 yılında Euler’in bu dizideki bir sonraki sayının asal olmadığını göstermesiyle Fermat’nın iddiasının doğru olmadığı ortaya çıkıyor. Günümüzde hala “Bu ilk beşi dışında başka asal Fermat sayısı var mı? Varsa, kaç tanedir? Sonsuz tane olabilir mi?” gibi sorular cevap bekliyor.

Fermat sayılarına benzerliğini düşünerek hangi $n$ sayıları için $2^n-1$ sayısının asal olduğunu da sorabiliriz. Bu sorunun cevabını Öklid’in de merak ettiğini biliyoruz. Öklid’in bu sayılara ilgisi mükemmel sayı arayışından geliyor. Kendisinden küçük pozitif bölenlerinin toplamı kendisine eşit olan sayılara mükemmel sayı deniyor, mesela 6=1+2+3.

Öklid bir $N$ çift sayısının mükemmel olması için $2^n-1$ bir asal ve $N=2^{n-1}(2^n-1)$ olacak biçimde bir $n$ sayısının var olmasının yeterli ve gerekli olduğunu ispatlıyor. Yani $2^n-1$ biçiminde bir asal sayı bulduğumuzda hemen bir mükemmel sayı oluşturabiliyoruz.

1644’de Mersenne 257’ye kadarki tüm n değerlerinden sadece ve tam olarak $n$ = 2, 3, 5, 7, 13, 17, 19, 31, 67, 127 ve 257 değerlerinin bize asal sayı verdiğini iddia ediyor. Bu listenin hata içerip içermediğinin, tam olup olmadığının anlaşılması yüzyıllar sürüyor. Aralarında yine Euler’in de bulunduğu pek çok matematikçinin çalışmaları sonucunda 1947’de listenin: $n$ = 2, 3, 5, 7, 13, 17, 19, 31, 61, 89, 107 ve 127 biçiminde olması gerektiğini anlıyoruz. Listesi hatalı ve eksik olsa da bu ilginç serüven $2^n-1$ biçimindeki sayılara Mersenne sayıları, bunların asal olanlarına da Mersenne asalı denmesini sağlamış.

Bir $n$ sayısının kendisi asal değilse (diyelim ki $n>a$, $b>1$ olmak üzere $n=a\times b$ olsun), $2^n-1$ sayısının da asal olamayacağını görmek kolay ($2^n-1$ hem $2^a-1$, hem de $2^b-1$ sayısına bölünür). Demek ki Mersenne asallarını asal kuvvetlere denk gelen Mersenne sayıları arasında arayacağız. Fakat $2^n-1$ sayısının asal olması için $n$ sayısının da asal olması gerekli, ama bu yeterli değil. Örneğin 11 asal olmasına rağmen $2^{11}-1=2047=23\times 89$ asal sayı değildir. Mersenne sayılarının tam olarak ne zaman asal olduğunu belirlemek için Lucas-Lehmer testi adıyla bilinen, sayıların büyüklüğü de göz önünde bulundurulduğunda çok verimli diyebileceğimiz bir test var: $2^n-1$ Mersenne sayısının asal olup olmadığını test etmek için öncelikle $n$’in asal olduğunu kontrol edelim ($2^n-1$ ile kıyasla $n$ çok daha küçük bir sayı). Eğer $n$ asal ise,

$s_0=4$, ve $i\ge 0$ için $s_{i+1}=s_i^2-2$

kuralı ile bir sayı dizisi tanımlayalım. Eğer $2^n-1$ asalsa $s_{p-2}$ sayısı $2^n-1$’e bölünür. Eğer $s_{p-2}$ sayısı $2^n-1$’e bölünürse $2^n-1$ asaldır.

GIMPS-Büyük Internet Mersenne Asal Arayışı

Mersenne sayıları, üstel olarak arttığından özellikle büyük asallar bulmak için iyi adaylar. Dahası, Lucas-Lehmer testi bize Mersenne sayılarının asal olup olmadığını belirlemek için çok verimli bir yöntem sunuyor. Bu algoritma ve bilgisayar yardımı ile büyük asal sayı avına çıkabiliriz. Great Internet Mersenne Prime Search (GIMPS-Büyük Internet Mersenne Asal Arayışı) de tam olarak bunu yapıyor:

Bilgisayarınıza indireceğiniz ufak bir program ile bilgisayarınızı kullanmadığınızda arka planda Mersenne asalları arayışına katkıda bulunabiliyorsunuz. Hatta bir para ödülü de var.  200 bin’den fazla kullanıcısı olan projede dünyanın dört bir yanına dağılmış 2 milyona yakın işlemci ile Mersenne asalları aranıyor.

İşte yukarıda bahsettiğimiz “En büyük asal sayı bulundu” haberleri de GIMPS ile ilgili: İspatladığımız gibi en büyük asal sayı olmamakla birlikte büyük asal sayı bulma yarışında ne zaman yeni bir rekor kırılsa haber oluyor. 21 Ekim 2024’te çıkan haber de yeni bulunan bir Mersenne asalı ile ilgili.[1]

GIMPS projesi ile yeni bir Mersenne asalı bulundu:$$2^{136.279.841}-1$$

Meraklıları için toplam 41.024.320 basamaklı bu sayıyı GIMPS sayfasından indirmek mümkün. Böylelikle bilinen 52. Mersenne asalı olan bu sayı altı yıl önce bulunan eski rekortmen$$2^{82.589.933}-1$$sayısından yaklaşık 16 milyon daha fazla basamağa sahip. Yaklaşık 42 MB yer kaplıyor. Basılı halde ise A4 kağıdı boyutunda kabaca 10.000 sayfalı bir kitabı dolduruyor (En büyük asalın bulunduğunu iddia edenleri bu 10.000 sayfalık kitapla kovalamak gerekir!)

Peki büyük asallar bulmak niçin önemli? Aslında pek de önemli değil. Ne de olsa asallar sonsuz. Büyük asallar bulmak her alanda olduğu gibi insanlığın “en büyük”, “en uzun”, “en fazla” olanı bulma sevdası ile alakalı biraz. Asallar da bu yarış ve sıralama ortamından nasibini almış. Durum virgülden sonra sonsuz basamağı olan pi sayısının hep daha fazla basamağını bulma (ve hatta bunları ezberleme!) yarışından pek farklı değil.

Belki asalların şifreleme için kullanıldığını ve bu sebeple büyük asalların önemli olduğunu duymuşsunuzdur. Daha güvenli sistemler için daha büyük asallara ihtiyaç duyulduğu doğru olsa da kullanılan ve günümüz standartlarında güvenli bulunan asal sayılar birkaç yüz basamaklı. Yani ihtiyaçlar 41 milyon basamak mertebelerinden çok uzak.

Peki matematik açısından büyük asal sayılar bulmanın hiç mi anlamı yok? Elbette var. Büyük asal sayıların kendileri neredeyse önemsiz olmakla birlikte bu arayışın tetikleyeceği yeni çalışmalar, bunları ararken geliştirilecek yeni fikirler, 21 Ekim 2024’te kırılan yeni asal rekoru çoktan unutulduktan sonra bile insanlığın ortak düşünsel hazinesinin bir parçası olacaktır. Bunun en iyi örneklerinden biri Fermat’nın Son Teoremi olarak bilinen 350 sene kadar çözülememiş, çoğu okurumuzun bildiği bir soru. Bu masum görünümlü soru 20. yüzyılın başlarında cebirde çok önemli bir yer tutan ideal kavramının ortaya çıkmasını, cebirsel sayılar kuramının geliştirilmesini sağladı ve Andrew Wiles’in ispatı ve onu izleyen gelişmelerle Taniyama-Shimura-Weil sanısının ispatına ve sayılar kuramının 21. yüzyıldaki gelişimine yön verdi. Sorunun cevabı her ne kadar sayılar kuramı açısından çok önemli olmasa da bu sonuca ulaşabilmek için geliştirilen yeni matematiksel fikir, teori ve tekniklerin sayılar kuramına önümüzdeki yüzyıl boyunca da yön verecek nitelikte olduğunu söylemek abartı olmaz. Fermat sorusu bir gün unutulsa bile çözümü için geliştirilen fikirler matematikteki önemli yerlerini çoktan almış olacaklardır.

Bu arada evinden bilime katkı sağlamak isteyenler için GIMPS’e benzer başka dağılımlı işlem projeleri olduğunu da belirtelim:

https://www.wikizero.com/en/List_of_distributed_computing_projects

Burada asteroidler hakkındaki bilgimizi arttırma, CERN’deki ATLAS deneylerine katkı sağlama, iklim modellerini iyileştirme, pulsar arama, 2. Dünya Savaşı’ndan kalan çözülmemiş Enigma mesajlarını çözme, RNA yapısını inceleme gibi birçok farklı proje mevcut.

Güzel hesaplamalar dileriz!

Alp Bassa (Boğaziçi Üniversitesi Matematik Bölümü öğretim üyesi)
Ayhan Dil (Akdeniz Üniversitesi Matematik Bölümü öğretim üyesi)
Özer Öztürk (Mimar Sinan Güzel Sanatlar Üniversitesi Matematik Bölümü öğretim üyesi)

Eğitim : Ödev / Ders / Proje / Tez / Çizim